The 20 physics questions given below are both interesting and highly
challenging. You will likely have to take some time to work through
them. These questions go beyond the typical problems you can expect to
find in a physics textbook. Some of these physics questions make use of
different concepts, so (for the most part) there is no single formula or
set of equations that you can use to solve them. These questions make
use of concepts taught at the high school and college level (mostly
first year).
It is recommended that you persist through these physics questions, even
if you get stuck. It's not a race, so you can work through them at your
own pace. The result is that you will be rewarded with a greater
understanding of physics.
discuss your answers in the comments
Problem # 1
A crank drive mechanism is illustrated below. A uniform linkage
BC of length
L connects a flywheel of radius
r (rotating about fixed point
A) to a piston at
C that slides back and forth in a hollow shaft. A variable torque
T
is applied to the flywheel such that it rotates at a constant angular
velocity. Show that for one full rotation of the flywheel, energy is
conserved for the entire system; consisting of flywheel, linkage, and
piston (assuming no friction).
Note that gravity
g is acting downwards, as shown.
Even though energy is conserved for the system, why is it a good idea to
make the components of the drive mechanism as light as possible (with
the exception of the flywheel)?
Problem # 2
An engine uses compression springs to open and close valves, using cams.
Given a spring stiffness of 30,000 N/m, and a spring mass of 0.08 kg,
what is the maximum engine speed to avoid “floating the valves”?
During the engine cycle the spring is compressed between 0.5 cm (valve
fully closed) and 1.5 cm (valve fully open). Assume the camshaft rotates
at the same speed as the engine.
Floating the valves occurs when the engine speed is high enough so that
the spring begins to lose contact with the cam when the valve closes. In
other words, the spring doesn’t extend quickly enough to maintain
contact with the cam, when the valve closes.
For simplicity, you may assume that Hooke’s Law applies to the spring,
where the force acting on the spring is proportional to its amount of
compression (regardless of dynamic effects).
You may ignore gravity in the calculations.
Problem # 3
An object is traveling in a straight line. Its acceleration is given by
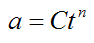
where
C is a constant,
n is a real number, and
t is time.
Find the general equations for the position and velocity of the object as a function of time.
Problem # 4
In archery, when an arrow is released it can oscillate during flight. If
we know the location of the center of mass of the arrow (
G) and
the shape of the arrow at an instant as it oscillates (shown below), we
can determine the location of the nodes. The nodes are the “stationary”
points on the arrow as it oscillates.
Using a geometric argument (no equations), determine the location of the nodes.
Assume that the arrow oscillates in the horizontal plane, so that no
external forces act on the arrow in the plane of oscillation.
Problem # 5
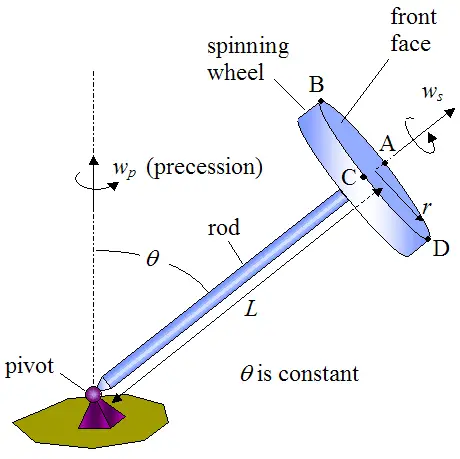
A gyroscope wheel is spinning at a constant angular velocity
ws while precessing about a vertical axis at a constant angular velocity
wp. The distance from the pivot to the center of the front face of the spinning gyroscope wheel is
L, and the radius of the wheel is
r. The rod connecting the pivot to the wheel makes a constant angle
θ with the vertical.
Determine the acceleration components normal to the wheel, at points A, B, C, D labeled as shown.
Problem # 6
When a vehicle makes a turn, the two front wheels trace out two arcs as
shown in the figure below. The wheel facing towards the inside of the
turn has a steering angle that is greater than that of the outer wheel.
This is necessary to ensure that both front wheels smoothly trace out
two arcs, which have the same center, otherwise the front wheels will
skid on the ground during the turn.
During a turn, do the rear wheels necessarily trace out the same arcs as
the front wheels? Based on your answer, what are the implications for
making a turn close to the curb?
Problem # 7
A horizontal turntable at an industrial plant is continuously fed parts
into a slot (shown on the left). It then drops these parts into a basket
(shown on the right). The turntable rotates 180° between these two
stages. The turntable briefly stops at each 1/8
th of a turn in order to receive a new part into the slot on the left.
If the rotational speed of the turntable is
w radians/second, and the outer radius of the turntable is
R2, what must be the inner radius
R1 so that the parts fall out of the slot and into the basket, as shown?
Assume:
• The angular speed
w of the turntable can be treated as constant
and continuous; which means you can ignore the brief stops the
turntable makes at each 1/8
th of a turn.
• The location of the basket is 180° from the feed location.
• The slots are very well lubricated so that there is no friction between the slot and part.
• The parts can be treated as particles, which means you can ignore their dimensions in the calculation.
• The slots are aligned with the radial direction of the turntable.
Problem # 8
A flywheel for a single piston engine rotates at an average speed of
1500 RPM. During half a rotation the flywheel has to absorb 1000 J of
energy. If the maximum permissible speed fluctuation is ± 60 RPM, what
is the minimum rotational inertia of the flywheel? Assume there is no
friction.
Problem # 9
An aluminum extrusion process is simulated numerically with a computer.
In this process, a punch pushes an aluminum billet of diameter
D through a die of smaller diameter
d. In the computer simulation, what is the maximum punch velocity
Vp
so that the net dynamic force (predicted by the simulation) acting on
the aluminum during extrusion is at most 5% of the force due to
deformation of the aluminum? Evaluate for a specific case where
D = 0.10 m,
d = 0.02 m, and the density of aluminum is
ρ = 2700 kg/m
3.
Hint:
The extrusion of the aluminum through the die is analogous to fluid
flowing through a pipe which transitions from a larger diameter to a
smaller diameter (e.g. water flowing through a fireman’s hose). The net
dynamic force acting on the fluid is the net force required to
accelerate the fluid, which occurs when the velocity of the fluid
increases as it flows from the larger diameter section to the smaller
diameter section (due to conservation of mass).
Problem # 10
A child on a horizontal merry-go-round gives an initial velocity
Vrel to a ball. Find the initial direction and velocity
Vrel
of the ball relative to the merry-go-round so that, relative to the
child, the ball goes around in a perfect circle as he’s sitting on the
merry-go-round. Assume there is no friction between merry-go-round and
ball.
The merry-go-round is rotating at a constant angular velocity of
w radians/second, and the ball is released at a radius
r from the center of the merry-go-round.
Problem # 11
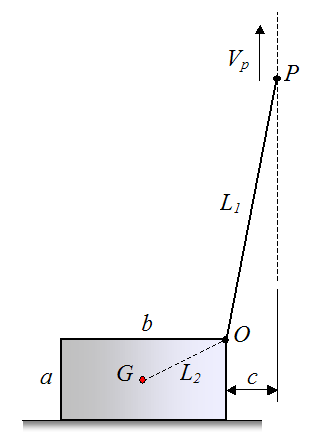
A heavy pump casing with a mass
m is to be lifted off the ground
using a crane. For simplicity, the motion is assumed to be
two-dimensional, and the pump casing is represented by a rectangle
having side dimensions
ab (see figure). A cable of length
L1 is attached to the crane (at point
P) and the pump casing (at point
O). The crane pulls up vertically on the cable with a constant velocity
Vp.
The center of mass
G of the pump casing is assumed to lie in the center of the rectangle. It is located at a distance
L2 from point
O. The right side of the pump casing is located at a horizontal distance
c from the vertical line passing though point
P.
Find the maximum cable tension during the lift, which includes the part
of the lift before the pump casing loses contact with the ground, and
after the pump casing loses contact with the ground (lift off). In this
stage the pump casing swings back and forth.
Evaluate for a specific case where:
a = 0.4 m
b = 0.6 m
c = 0.2 m
L1 = 3 m
m = 200 kg
IG = 9 kg-m
2 (rotational inertia of pump casing about
G)
Assume:
• The friction between the pump casing and ground is high enough so that
the pump casing does not slide along the ground (towards the right),
before lift off occurs.
• Before lift off occurs, dynamic effects are negligible.
• The velocity
Vp is fast enough so that the bottom of the pump casing swings clear of the ground after lift off occurs.
• For purposes of approximating the cable tension, you can model the
system as a regular pendulum during swinging (you can ignore double
pendulum effects).
• The mass of the cable can be neglected.
Problem # 12
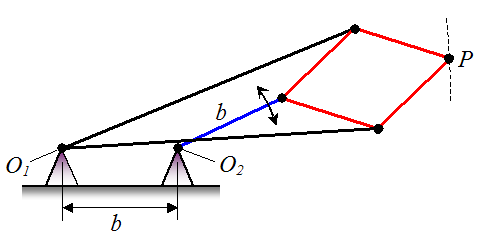
A linkage arrangement is shown below. The pin joints
O1 and
O2 are attached to a stationary base and are separated by a distance
b.
The linkages of identical color have the same length. All linkages are
pin jointed and allow for rotation. Determine the path traced by the end
point
P as the blue linkage of length
b rotates back and forth.
Why is this result interesting?
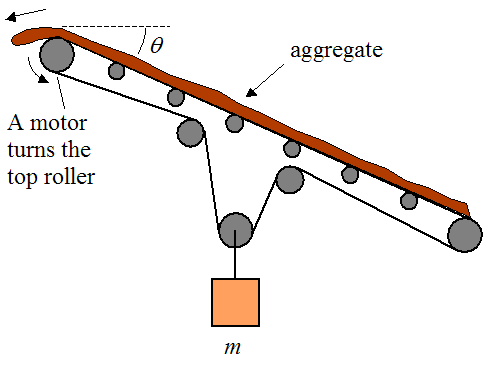
Problem # 13
A conveyor belt carrying aggregate is illustrated in the figure below. A
motor turns the top roller at a constant speed, and the remaining
rollers are allowed to spin freely. The belt is inclined at an angle
θ. To keep the belt in tension a weight of mass
m is suspended from the belt, as shown.
Find the point of maximum tension in the belt. You don’t have to calculate it, just find the location and give a reason for it.
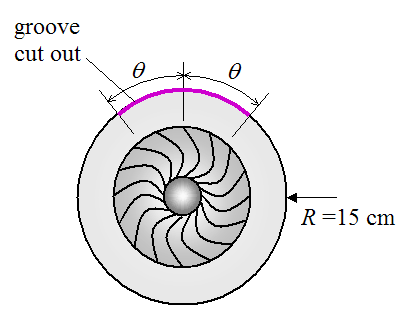
Problem # 14
A quality test has determined that a pump impeller is too heavy on one
side by an amount equal to 0.0045 kg-m. To correct this imbalance it is
recommended to cut out a groove around the outer circumference of the
impeller, using a milling machine, on the same side as the imbalance.
This will remove material with the intent of correcting the imbalance.
The dimension of the groove is 1 cm wide and 1 cm deep. The groove will
be symmetric with respect to the heavy spot. How far around the outer
circumference of the impeller should the groove be? Specify the answer
in terms of
θ. Hint: Treat the groove as a thin ring of material.
The outer radius of the impeller, at the location of the groove, is 15 cm.
The impeller material is steel, with a density of
ρ = 7900 kg/m
3.
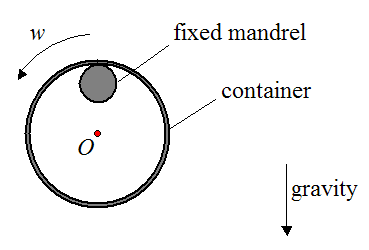
Problem # 15
As part of a quality check, an axisymmetric container is placed over a
very well lubricated fixed mandrel, as shown below. The container is
then given an initial pure rotation
w, with no initial
translational motion. What do you expect to see if the center of mass of
the container is offset from the geometric center
O of the container?
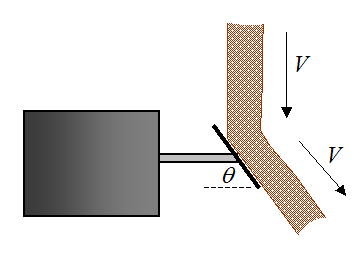
Problem # 16
A stream of falling material hits the plate of an impact weigher and the
horizontal force sensor allows the mass flow rate to be calculated from
this. If the speed of the material just before it strikes the plate is
equal to the speed of the material just after it strikes the plate,
determine an equation for the mass flow rate of the material, based on
the horizontal force readout on the sensor. Ignore friction with the
plate.
Hint: This can be treated as a fluid flow problem.
Problem # 17
The SunCatcher is a Stirling engine that is powered by solar energy. It
uses large parabolic mirrors to focus sunlight onto a central receiver,
which powers a Stirling engine. In the parabolic mirror you can see the
reflection of the landscape. Why is the reflection upside down?
Source: http://www.stirlingenergy.com
Problem # 18
On a cold, dry winter day your glasses fog up when you go indoors after being outside for a while. Why is that?
And if you go back outside with your glasses still fogged up, they quickly clear up. Why is that?
Problem # 19
In an astronaut training exercise, an airplane at high altitude travels
along a circular arc in order to simulate weightlessness for its
passengers. Explain how this is possible.
Problem # 20
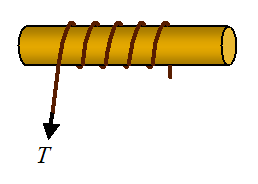
A rope is wrapped around a pole of radius
R = 3 cm. If the tension on one end of the rope is
T = 1000 N, and the coefficient of static friction between the rope and pole is
μ = 0.2, what is the minimum number of times the rope must be wrapped around the pole so that it doesn’t slip off?
Assume that the minimum number of times the rope must be wrapped around
the pole corresponds to a tension of 1 N on the other end of the rope.
Begin each problem with what you know, the
GIVEN material and the GIVEN amount in whatever units it is given.
2NH3
The MVG is the "molar volume of gas at STP." The
MR is the mol ratio. Notice the numbers in
blue in the mol ratio. Those numbers come from the
coefficients in the balanced chemical equation.
The math is: 89.6 ÷ 22.4 ÷ 3 x 2 x 22.4 =
The math is: 10 ÷ 100.1 x 22.4 =
The math is: 11.2 ÷ 22.4 x 65.4 =
C)
and 1 atm.
CO2
ho of us would not be glad to lift
the veil behind which the future lies
hidden; to cast a glance at the next
advances of our science and at the
secrets of its development during
future centuries?"
